What is Markov Chain?

Markov Chain is a way of solving real-life problems using probabilities

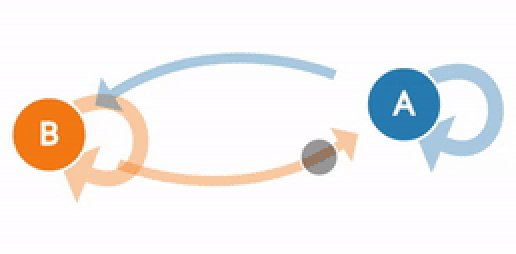
My favourite thing about Markov Chain?

It is called Markov Chain but in real sense, it is mostly known as Discrete-Time Markov Chain. Why is this so? Everything is under our control. Suppose you own a really big restaurant named: Chain restaurant. You sell rice, beans and egg. Now this food you sell can be referred to as the state space. You cannot order all at the same time because Chain restaurant is for the rich and wealthy.

What happens is this at each point a food is ordered, it takes a certain time. Now this time is very important so we know which food was ordered first, next and last. There are different variations of this time too.

Why do you need to learn Markov Chain?

Markov Chains can be applied to solve problems related to finance, economics, communication theory, genetics and economics to solve problems.

Can Markov Chain solve all type of problems?

No, and this is because Markov Chain depends only on the previous event that occurred. For instance; failing the last course you took this semester, does this mean you will fail the first course you will take next semester?

Also you can either choose to implement a Markov Chain using a Dictionary that contains the probability of all the likely state transitions or you define a Transition Matrix that contains all the state transitions. When there are few transitions, you can make use of the Dictionary approach. But when there are a lot of state transitions then this method is not advisable and it is better to make use of a transition matrix.

How are transition probabilities computed?

They are usually computed over a long sequence of data

For example: Let’s say, we would know the sequence of sunny, cloudy and rainy days for a long duration, lets say 2 years. If in the 2 years, the total number of sunny days is 100, and out of that if the next day was a cloudy day 20 percent of the times, then the transition probability of Sunny -> Cloudy would be 20/100 = 0.2. Likewise, all possible combinations are computed and the transition probability matrix is formed.

References

1. Markov Chains in Python: Beginner Tutorial: https://www.datacamp.com/community/tutorials/markov-chains-python-tutorial
2. Introduction to Markov Chain https://towardsdatascience.com/introduction-to-markov-chains-50da3645a50d
3. Markov Chain Analysis and Simulation using Python https://towardsdatascience.com/markov-chain-analysis-and-simulation-using-python-4507cee0b06e
4. Markov Chain in Python https://www.upgrad.com/blog/markov-chain-in-python-tutorial/
5. Gentle Introduction to Markov Chain https://www.machinelearningplus.com/markov-chain/